|
|
|
This appendix formalizes the dual usage and unified interpretation of Effective Acceleration (aᵉᶠᶠ) and the Effective Transformation Coefficient (aᵉᶠᶠ) within Extended Classical Mechanics (ECM). While the former is conventionally expressed as a kinematic quantity for massive particles governed by Mᴍ, the latter generalizes the same coefficient for systems where dynamical evolution is governed by mass–potential restructuring, negative-apparent-mass displacement, or frequency-based propagation, including photons and electromagnetic quanta. This document establishes the continuity between the numerical constant 6 × 10⁸ m/s² derived from standard ECM kinematic geometry and its generalized interpretation as a transformation coefficient in dynamic frequency-governed systems. The appendix clarifies that both forms describe the same ECM quantity under different physical domains and that photon propagation, though initiating with the same effective-acceleration value at emission, evolves according to the transformation formulation throughout its path to rmax.
Extended Classical Mechanics, Effective Acceleration, Effective Transformation Coefficient, Negative Apparent Mass, Photon Dynamics, Mass–Potential Transition, Frequency-Governed Motion, rmax, Mass Displacement, ECM Cosmology
Extended Classical Mechanics (ECM) distinguishes between mechanically measurable accelerations and transformation-driven restructuring effects that emerge from mass–potential interactions in both particle-scale and cosmological contexts. The traditional ECM expression for Effective Acceleration, aᵉᶠᶠ = 2Δd/(Δt)², yields the characteristic value 6 × 10⁸ m/s² under standard photon-emission geometry. This value continues to play a fundamental role across ECM formulations, including those involving frequency scaling, reversible mass–energy dynamics, and negative apparent mass.
To account for cases where displacement is governed not by kinematic acceleration but by energetic restructuring—particularly for photons and systems exhibiting −Mᵃᵖᵖ—the same ECM quantity is reinterpreted as the Effective Transformation Coefficient. This appendix establishes the definitions, their domain-specific usage, and the internal continuity required for consistent ECM application.
For any particle possessing real mass Mᴍ, the coefficient aᵉᶠᶠ operates as a generalized acceleration parameter emerging from ECM’s mass–potential structure. It governs the dynamics associated with negative apparent mass displacement (−Mᵃᵖᵖ), effective mass reconfiguration, and momentum exchange in gravitational or non-gravitational environments.
Its classical computation remains:
This numerical value is preserved across all ECM treatments involving mechanical particles (including electrons), where displacement is geometry-driven.
For dynamic entities such as photons—whose propagation arises from frequency-governed mass-potential transitions rather than inertial acceleration—the same coefficient is expressed as the Effective Transformation Coefficient.
Photons achieve aᵉᶠᶠ = 6 × 10⁸ m/s² at emission, but their subsequent propagation is fully governed by transformation-driven restructuring as the system evolves toward rₘₐₓ. This formulation aligns with the ECM relation c = fₚₕₒₜₒₙ λₚₕₒₜₒₙ and the frequency-origin of kinetic energy
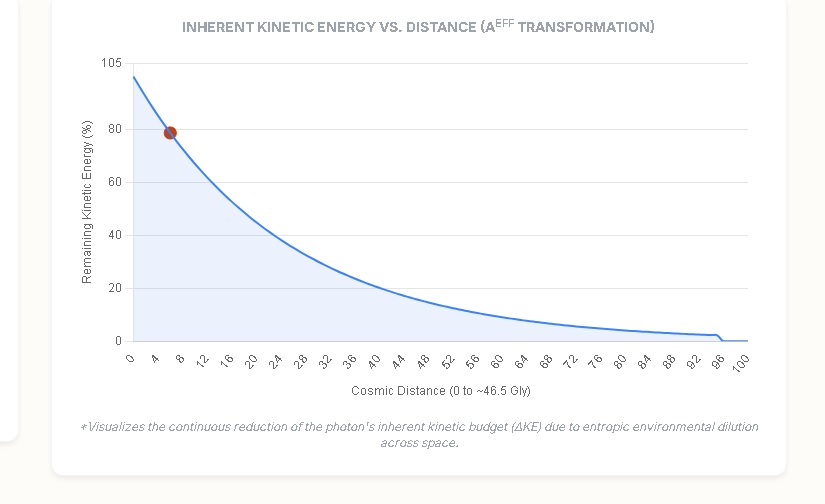
Figure 1: Reduction in the photon's inherent kinetic energy (ΔKE) as a function of cosmic distance, governed by the Effective Transformation Coefficient (aᵉᶠᶠ). Illustrates ECM’s dual-mode interpretation: kinematic emission (aᵉᶠᶠ as acceleration) transitioning to environmental transformation-driven dilution (aᵉᶠᶠ as transformation coefficient).
Both names—Effective Acceleration and Effective Transformation Coefficient—refer to the same ECM quantity expressed in domain-appropriate language:
Thus the coefficient is universal, but context-specific in interpretation.
For photon-governed evolution:
This normalized coefficient is useful for comparative plots across photon, electron, and gravitational domains.
A frequent misunderstanding is the assumption that the shift from “Effective Acceleration” to “Effective Transformation Coefficient” implies a change in physical behaviour or a rejection of kinematic interpretation. ECM clarifies that both terms denote the same coefficient, whose numerical form remains unchanged. The distinction lies purely in whether propagation is governed by mechanical acceleration (Mᴍ-driven) or by frequency-origin mass–potential transition mechanisms (−Mᵃᵖᵖ-driven), as shown consistently across Appendix 12, Appendix 23, and Appendix 37.
This appendix establishes the unified interpretation of aᵉᶠᶠ across ECM. The coefficient retains its numerical identity in all contexts but expresses different physical roles depending on whether motion is driven by mass-inertia or by mass–potential transformation. This continuity ensures that ECM retains a self-consistent energetic structure across photons, electrons, gravitational mediation, and cosmological scaling up to rₘₐₓ.